| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
- 스프린트 리뷰
- testbuilder
- supertest
- global scope
- Jest
- 코드스테이츠 1일차
- 슈도코드
- version control system
- 호이스팅
- nvm 설치
- node 설치
- 코플릿
- indexof
- for of
- JavaScript Runtime
- package.json
- dot notation
- foreach
- 2번째 페어
- for in
- Splice
- Bracket Notation
- local scope
- immutable
- npm 설치
- TIL
- 코딩게임
- includes
- javascript 기초
- HTML 태그 모음
- Today
- Total
Honey-Programming
[자료구조] Graph, Tree, BST 본문
1. Graph


- Graph 란 Node(또는 정점 vertex) 와 Node들을 잇는 Edge으로 구성되어 있는 데이터 구조이다.
- 그래프는 무방향일 수 있음
- 간선에 의해 연결된 2개의 노드가 대칭일 수 있다는 의미
- 방향성(directed)을 가질 수도 있는데, 이는 비대칭 관계를 의미
1) 진입 차수 & 진출 차수
진입 차수(In-degree) : 방향 그래프에서 외부 노드에서 오는 간선의 수를 의미한다. (다른 말 '내차수')
진출 차수(Out-degree) : 방향 그래프에서 외부 노드에서 오는 간선의 수를 의미한다. (다른 말 '외차수')
2) 그래프(Graph)의 구현방식 (인접 행렬, 인접 리스트)
인접 리스트(Adjacency list)

- 노드에 연결되어 있는 노드들을 리스트로 표현한 것.
방향, 가중치 그래프가 주어졌을 때, 연결되어 있는 상황을 인접리스트로 출력할 수 있다. - 연결된 간선의 정보만을 저장하여 O(E)의 공간을 요구하여 공간 효율성이 우수하지만
두 정점이 서로 연결되어 있는 지 확인하기 위해 O(v)의 시간을 요구한다.
인접 행렬(Adjacency matrix)

- 인접행렬은 노드를 2차원 배열로 만든 것이다.
무방향 그래프에 가중치가 없는 그래프일 경우 인접행렬로 표현할 수 있다. - 모든 정점들의 연결여부를 저장하여 O(V2)의 공간을 요구하므로 공간 효율성이 떨어지지만
두 정점이 서로 연결되어 있는지 확인하기 위해 O(1)의 시간을 요구한다.
3) Graph method
- .addNode() : 새로운 node를 생성하여 그래프에 노드를 추가
- .contains() : node.value가 존재하는지 확인하고, boolean 값을 출력한다
- .removeNode() : node를 삭제하고, 연결되어 있는 간선 또한 제거한다.
- .addEdge(fromNode, toNode) : fromNode 와 toNode 사이의 간선(edge)을 추가한다.
- .hasEdge(fromNode, toNode) : fromNode 와 toNode 사이의 간선(edge) 존재 확인하고, boolean 값을 출력한다.
- removeEdge(fromNode, toNode) : fromNode 와 toNode 사이의 간선(edge)을 삭제한다.
- forEachNode() : 각 노드를 한 번씩 호출하여 그래프를 통과한다.
2. Tree
모양은 Grahp 와 비슷하지만, 위에서 아래로 단방향성을 가지고 있다.
트리는 노드로 구성된 계층적 자료 구조
최상위 노트(root)를 만들고, 거기에 노드의 child를 추가하고, 거기에 또 추가하는 방식


- A, B, C, D 등 트리의 구성요소를 노드(node)
- 위 그림의 A처럼, 트리 구조에서 최상위에 존재하는 노드를 root
- 같은 depth에 존재하는 노드들은 sibling 관계
- 그림에서 A는 B와 C의 부모(parent) 이고, B와 C는 A의 자식(child)
- 노드와 노드를 잇는 선을 edge
- 자식이 없는 노드를 leaf
- 루트를 기준으로 다른 노드로의 접근하기 위한 거리를 depth
- 루트 높이의 깊이는 0
- 한 노드를 기준으로 leaf 노드까지의 최대높이를 height
- 트리 구조 대표적 예) DOM, dictionary, file system 등
Tree method
- insertNode(value) : 트리에 노드를 추가합니다
- contains(value) : 트리에 해당 노드가 존재하는지 여부를 반환한다.
3. BST (Binary Search Tree)

- 이진 탐색 트리는 최대 2개의 자식 노드만 가짐
- 트리 구조는 재귀적이어서, 자식 노드 역시 최대 2개의 자식을 가짐
- 이진 탐색 트리에서는 노드의 값이 정렬 방법에 따라 순서가 존재
- 노드의 왼쪽 서브트리에는 노드의 값보다 작은 값이, 오른쪽 서브트리에는 노드의 값보다 같거나 큰 값이 존재
1) 이진 탐색 트리 순회하는 방법
(1) 깊이 우선 탐색 (DFS : Depth-First Search)


위의 순회는 F → B → A → D → C → E → G → I → H 순으로 진행.
즉, 트리노드를 방문해서 값을 확인하고, children이 있는지 확인 후, 있으면
child node 들도 똑같이 값을 확인하고, children 확인하고, 하는 식으로 계속 반복되는 리커젼
장점 : 저장공간의 수요가 적다 / target이 깊숙한곳에 있다면 빠르게 searching 가능
단점 : 무한경로에 빠지는 경우가 있음 / 얻은 경로가 최적의 경로가 아닐수도 있음
(2) 너비 우선 탐색 (BFS : Breadth-First Search)
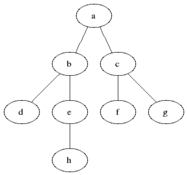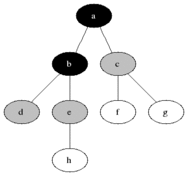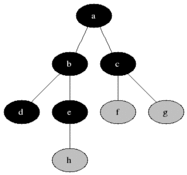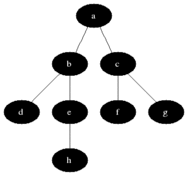

위의 순회는 F → B → G→ A →D → I → C→ E→ H 순으로 진행
각 노드에서 children 노드로 바로 넘어가는 것이 아니라,
children node를 배열에 넣어 depth별 노드들의 값을 한번에 확인함
장점 : 여러개의 경로가 있을경우 ( 최단 경로 찾기 가능 / 어느 한 경로가 무한경로에 빠지는경우에도 답 찾기 가능)
단점 : child의 갯수가 많을경우, 저장공간이 많이 필요 / 답이 깊숙히 있을경우 탐색에 오랜시간이 걸림
3) BST method
- insert(value) : 트리에 노드를 추가한다
- contains(value) : 트리에 해당 노드가 존재하는지 여부를 반환한다
- inorder(callback) : 이진 탐색 트리를 중위순회 합니다.
백 트래킹
풀이시간단축 을 위해 일정한 규칙(가능성)에 만족하지 않으면 그 하위 child은 배제 한 채 다른 Node 를 탐색하는 방법
'코드스테이츠 > Immersive' 카테고리의 다른 글
| Instantiation Patterns (0) | 2020.09.09 |
|---|---|
| [자료구조] stack, queue 구현하기 (0) | 2020.09.04 |
| [자료구조] Linked List, Hash Table (0) | 2020.09.03 |
| [자료구조] stack, queue (0) | 2020.09.03 |
| Git workflow (0) | 2020.09.01 |



